Basic movement mechanism and other game mechanics in videogames
Character movement (Documentation unfinished)
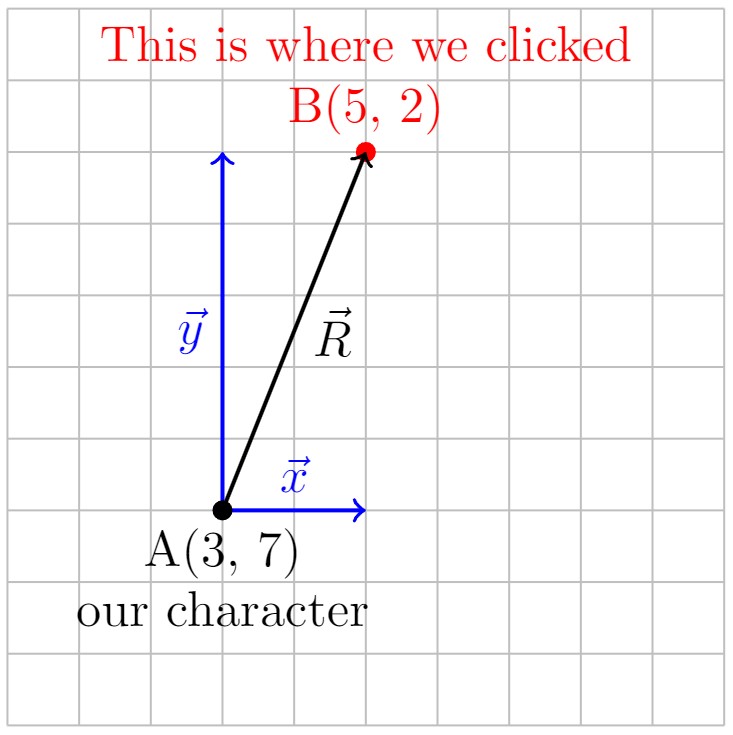
Lets start off by mentioning that the origin of our coordinate system resides on the upper left side of the screen, with the $x$ - axis pointing to the right, and $y$ - axis pointing down.
We can initialise a "character" or a "hero", by giving it some sort of initial position in the form of point $A$ with coordinates $(x_{A};y_{A})$. For simplicitys sake, we also model this character as a circle with some arbitrary radius $r$.
To move our character to the position of our mouseclick, we must store the coordinates of the mouseclick on the canvas. Lets represent the mouseclick as point $B$ with coordinates $(x_{B};y_{B})$.
Once the mouseclick position has been stored, we must then calculate the $\vec{x}$ and $\vec{y}$ projections of the distance $\vec{R}$ $(\vec{R}=\vec{x}+\vec{y})$ from point $A$ to point $B$.
This is simple to achieve by just taking the final position and subtracting the initial position of each component. Thus the equations look something like this
\[ \begin{cases}
\vec{x}=x_{B}-x_{A}\\
\vec{y}=y_{B}-y_{A}
\end{cases}
\]
In non-symbolic notation i.e code, it could look something like this
\[ \begin{array}{c}
distX=mouseX-charX\\
distY=mouseY-charY
\end{array} \]
Now assuming the canvas frame is being drawn in a loop, we can update the position of our character after the click with the following equations
\[ \begin{cases}
x_{A}=x_{A}+\vec{x}\\
x_{B}=x_{B}+\vec{y}
\end{cases}
\]
where $x_{A}$ and $x_{B}$ on the right hand side of the equation are the old stored values, and the ones on the left hand side are the new updated $x_{A}$ and $x_{B}$ values.
Since these equations dont really make much mathematical sense, let us instead rewrite this with code variables before we get beat up by a bunch of mathematicians.
\[ \begin{array}{c}
charX=charX+distX\\
charY=charY+distY
\end{array} \]
where $charX$ and $charY$ on the right hand side of the equation are the old stored values, and the ones on the left hand side are the new updated $charX$ and $charY$ values.
However notice that this system results in instant teleport/blink-like motion. If this is what you desire then this system works great, however we wish to model smooth motion from point A to point B instead.

To fix this, we should scale the full resultant vector $\vec{R}$ down. Ideally we would want to normalize it, so that the sum of the $\vec{x}$ and $\vec{y}$ components would be equal to $1$.
We can achieve this by using the Pythagorean theorem.
\[ c^{2}=a^{2}+b^{2} \]
Take the square root from both sides.
\[c=\sqrt{a^{2}+b^{2}} \]
Since we want the resultant vector $\vec{R}$ modulus $R$, or in this case the hypothenus, to be equal to $1$, then divide both sides by $c$.
\[ \dfrac{c}{c}=\dfrac{\sqrt{a^{2}+b^{2}}}{c} \]
This gives us
\[ 1=\dfrac{\sqrt{a^{2}+b^{2}}}{c}\]
which can be expanded further to
\[ 1=\sqrt{ \left( \dfrac{a}{c} \right)^{2}+\left( \dfrac{b}{c}\right)^{2} } \]
From here we see, that if we just take the $x$ and $y$ components, i.e the $\vec{x}$ and $\vec{y}$ component moduli, and divide each of them by the resultant vector $\vec{R}$ modulus $R$, then we achieve a set of downscaled vectors
which sum gives us a resultant vectors modulus of unit length $1$.
So mathematically
\[ \sqrt{ \left( \dfrac{x}{R} \right)^{2} + \left( \dfrac{y}{R} \right)^{2} } = 1\]
How is this useful? Well as mentioned previously, the resultant vector of the downscaled vector components now gives us a fixed unit length of $1$, regardless of how the vector is positioned.
And the number $1$ is useful because we can now multiply the vector components with any arbitrary magnitude (which in our case will be the movement speed, i.e step per frame).
Let us label the downscaled $x$ and $y$ components as $x_{n}$ and $y_{n}$, with $n$ standing for "normalized".
\[ \begin{cases}
x_{n}=\dfrac{x}{R}\\
\\
y_{n}=\dfrac{y}{R}
\end{cases} \]
Now if we want the movement "step" per frame (i.e movement speed) to be of magnitude $m$, we just multiply $x_{n}$ and $y_{n}$ both by $m$. Lets call the scaled up components $x_{s}$ and $y_{s}$.
\[ \begin{cases}
x_{s}=x_{n} \cdot m\\
y_{s}=y_{n} \cdot m
\end{cases} \]
Now, lets remind ourselves of what we wanted to achieve with this. The previous movement mechanism just teleported us to the position of our mouseclick and we wished to incorporate
a smooth step-like motion from point $A$ to point $B$.
To achieve this, we still use the same equations we defined for movement previously, but instead of using the $x$ and $y$ components corresponding to the
full distance from point $A$ to point $B$, we use the normalized and then scaled components $x_{s}$ and $y_{s}$ instead.
\[ \begin{cases}
x_{A}=x_{A}+x_{s}\\
x_{B}=x_{B}+y_{s}
\end{cases}
\]
Or in a less confusing manner
\[ \begin{array}{c}
charX=charX+x_{s}\\
charY=charY+y_{s}
\end{array} \]
where $charX$ and $charY$ on the right hand side is the characters coordinates in the previous iteration (frame), $charX$ and $charY$ on the left hand side of the equations is the new updated coordinates of our character, which we use
in the next iteration (frame) and $x_{s}$ with $y_{s}$ are the normalized and scaled step we do per each frame.

Its also worth mentioning, that we check the direction vector from the initial position point $A$ to the click position point $B$ each iteration as well, otherwise if we did that once at the start, we would just keep endlessly moving in the direction of the initially defined direction vector.
Dealing with jitter
We can however notice an issue. Whenever our character seemingly reaches the final position at point $B$ he starts to jitter.
This is due to the fact that each time we add a step components to our initial position components the sum might not add up percisely to the final position components at point $B$, forcing the vector to
flip its direction and move back the same number of steps. Then on the next iteration move forward again, then backwards, then forward, then backwards...and continues to do so infinitely.

To illustrtate this, let us consider a simple 1 dimensional case. Lets assume we're positioned on number "5" on the number line. We wish to reach number "15" as that is where
our user directs us to go. Lets also assume that our step each iteration is "3". So with each iteration we reach numbers: 5, 8, 11, 14 and then we jump right over 15 and reach 17 instead.
This flips the direction vector backwards and pushes us 3 steps back in the opposite direction, back to number 14. Then flips direction again and we reach number 17 etc.
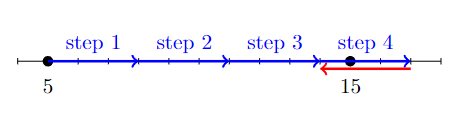
So in other words, we tend to over-step our final position, forcing us to go back and forth, resulting in a jittery effect. We could "fix" this by simply setting the step magnitude to "1",
but that would result in slower movement, and wouldnt really fix the issue eitherway, since our normalized $x$ and $y$ components arent integers in the first place.
Instead, we can just check wether the distance from our characters current position to the final position is smaller than half of the movement speed step.
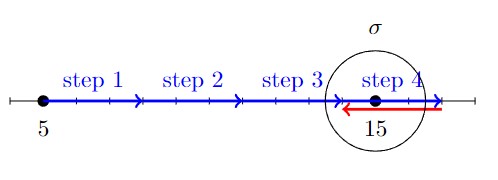
\[ (charX-finalX) < \dfrac{movementSpeed}{2} \]
This basically checks if we are within a certain level of tolerance \( \sigma \) of our final position, with movement speed being the tolerance \( \sigma \). In my code, I instead opted to check wether the distance
is larger than half movement speed step. If so then I just continued to animate the movement, and eventually when the distance was not larger, then I simply just stopped the animation process.
--- MORE TO COME LATER ---
MOVEMENT: click OR hold leftMouse anywhere INSIDE the interface. If your mouse happens to be outside the bounds of the interface, the movement STOPS, and continues only after the mouse has re-entered the interface.
DASH: press Spacebar to dash 100 pixels (5s cooldown) in the direction of your mouse cursor. Dash ability "bar" is seen at the bottom left of the screen.
Note: Its not really a "teleport/blink" but rather a temporary significant movement speed increase.
